Skip to contents

Functions calc_

functions_calc.Rmd

calc_ functions compute a certain value.

calc_acf

The goal of calc_acf is to compute the auto-correlation function, given by:

\[\frac{\sum_\limits{t = k+1}^{n}(x_t - \bar{x})(x_{t-k} - \bar{x})}{\sum_\limits{t = 1}^{n} (x_t - \bar{x})^2 },\] where:

  • \(x_t\) is a time series of length \(n\);
  • \(x_{t-k}\) is a shifted time series by \(k\) units in time;
  • \(\bar{x}\) is the average of the time series.

calc_acf(x)
#> # A tibble: 21 × 2
#>        acf   lag
#>      <dbl> <dbl>
#>  1  1          0
#>  2 -0.0893     1
#>  3  0.0206     2
#>  4 -0.0172     3
#>  5 -0.136      4
#>  6 -0.0597     5
#>  7  0.0324     6
#>  8  0.169      7
#>  9 -0.0795     8
#> 10  0.0389     9
#> # ℹ 11 more rows

If you pass a second vector in the argument y the cross-correlation will be computed instead:

\[\frac{n \left( \sum_\limits{t = 1}^{n}x_ty_t \right) - \left[\left(\sum_\limits{t = 1}^{n}x_t \right) \left(\sum_\limits{t = 1}^{n}y_t\right) \right]}{\sqrt{\left[n \left( \sum_\limits{t = 1}^{n}x_t^2 \right) - \left( \sum_\limits{t = 1}^{n}x_t \right)^2\right]\left[n \left( \sum_\limits{t = 1}^{n}y_t^2 \right) - \left( \sum_\limits{t = 1}^{n}y_t \right)^2\right]}},\] where:

  • \(x_t\) is a time series of length \(n\);
  • \(y_t\) is a time series of length \(n\).

calc_acf(x,y)
#> # A tibble: 33 × 2
#>        ccf   lag
#>      <dbl> <dbl>
#>  1  0.0755   -16
#>  2 -0.143    -15
#>  3  0.200    -14
#>  4 -0.234    -13
#>  5 -0.0297   -12
#>  6  0.0284   -11
#>  7  0.0534   -10
#>  8  0.111     -9
#>  9  0.0848    -8
#> 10 -0.179     -7
#> # ℹ 23 more rows

calc_association

The goal of calc_association is to compute associations metrics.

Contingency

Contingency is a measure of the degree to which two nominal variables are associated. It has a value between 0 and 1, with 0 indicating no relationship and 1 indicating perfect association, and is calculated as follows:

\[\sqrt{\frac{X^2}{n+X^2}},\]

where:

  • \(X^2\) the chi-square statistic;
  • \(n\) is the sample size.
calc_association(mtcars$am,mtcars$vs,type = "contingency")
#> [1] 0.1660092

Cramér’s V

Cramér’s V is a measure of the degree to which two nominal variables are associated. It has a value between 0 and 1, with 0 indicating no relationship and 1 indicating perfect association, and is calculated as follows:

\[\sqrt{\frac{X^2}{n\min(r-1,c-1)}},\]

where:

  • \(X^2\) the chi-square statistic;
  • \(n\) is the sample size;
  • \(r\) is the number of rows in the contingency table;
  • \(c\) is the number of columns in the contingency table.
calc_association(mtcars$am,mtcars$vs,type = "cramers-v")
#> [1] 0.1042136

Phi

Phi is a measure of association between two nominal dichotomous variables that takes into account a marginal table of the variables given by:

y = 0 y = 1 Total
x = 0 \(n_{00}\) \(n_{01}\) \(n_{0.}\)
x = 1 \(n_{10}\) \(n_{11}\) \(n_{1.}\)
Total \(n_{.0}\) \(n_{.1}\) \(n\)

Then the phi coefficient is given by:

\[\frac{n_{11}*n_{00} - n_{10}*n_{01} }{\sqrt{n_{1.}*n_{0.}*n_{.1}*n_{.0}}}.\]

calc_association(mtcars$am,mtcars$vs,type = "phi")
#> [1] 0.1700405

calc_auc

The goal of calc_auc is to compute the area under a curve (AUC).

x <- seq(-3,3,l = 100)

y <- dnorm(x)

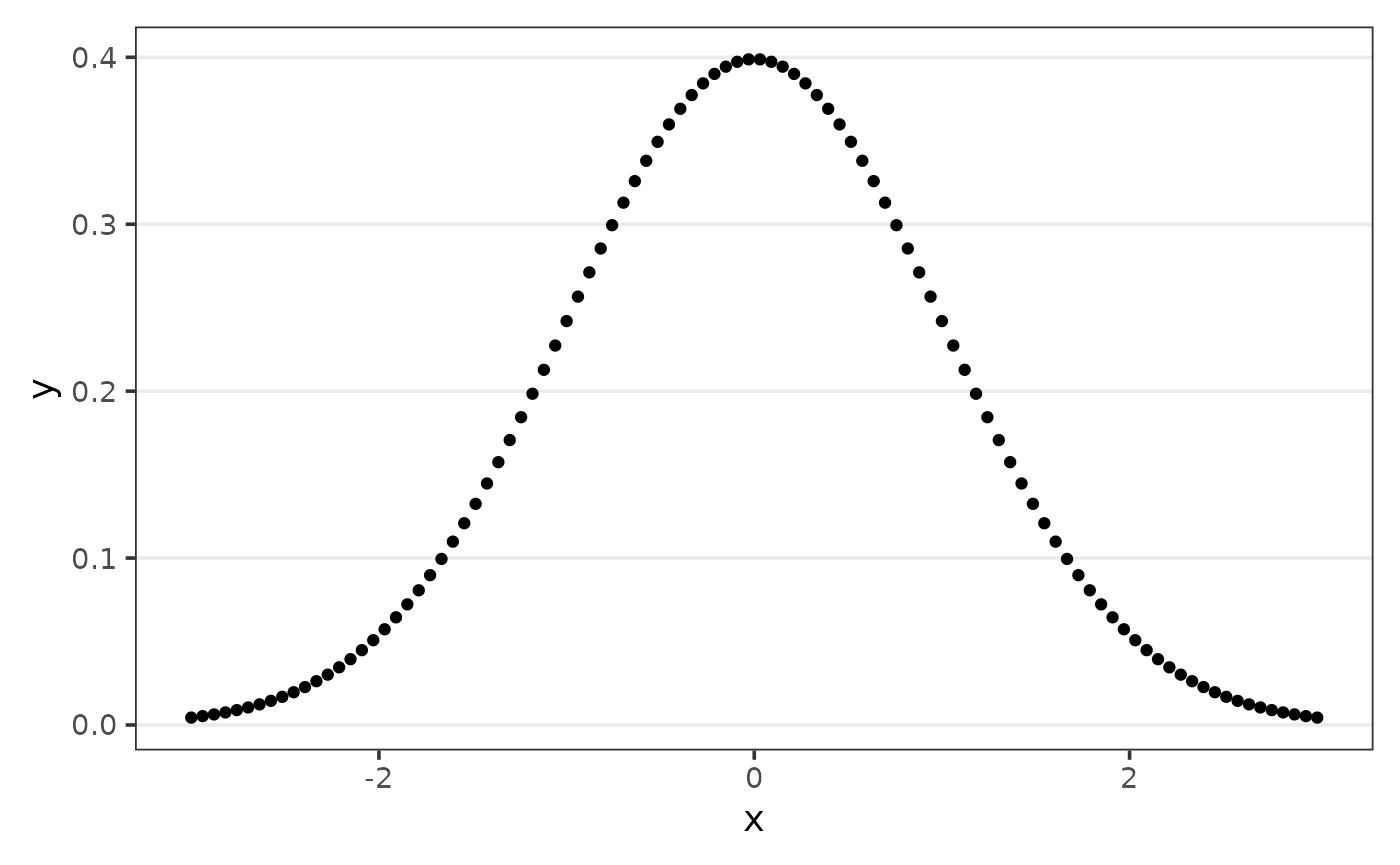
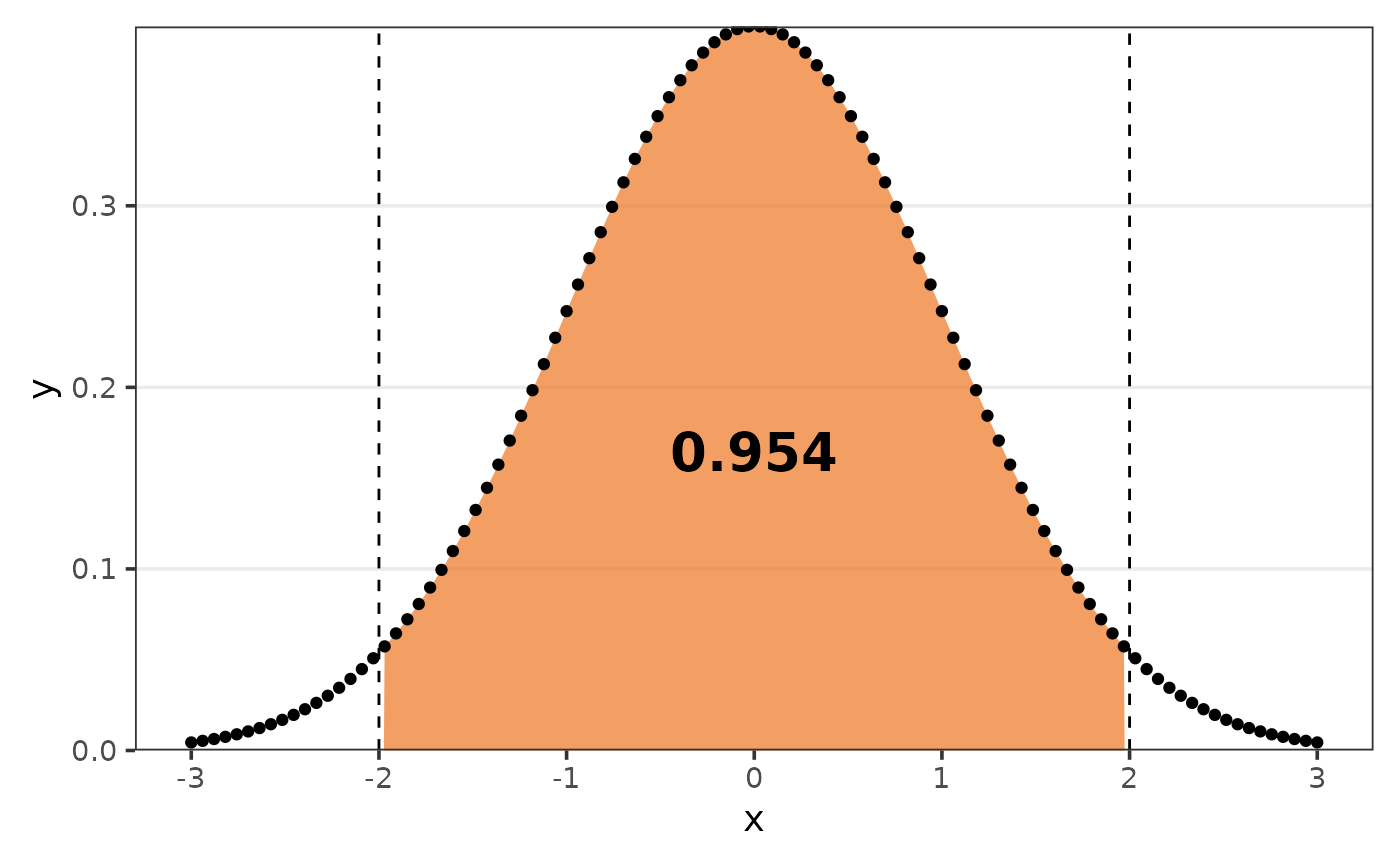
The function default compute the area considering the range of x.

#from min to max of x
range(x)
#> [1] -3  3

calc_auc(x,y)
#> [1] 0.9972835

But you can define the argument limits to get the AUC of that respective range.

#from -2 to 2
calc_auc(x,y,limits = c(-2,2))
#> [1] 0.9544345

#from -1 to 1
calc_auc(x,y,limits = c(-1,1))
#> [1] 0.6825416

calc_combination

The goal of calc_combination is to compute the number of combinations/permutations. Given that there are a total of \(n\) observations and that \(r\) will be chosen.

Order matter with repetition

\[n^r.\]

calc_combination(n = 10,r = 4,order_matter = TRUE,with_repetition = TRUE)
#> [1] 10000

Order matter without repetition

\[\frac{n!}{(n-r)!}.\]

calc_combination(n = 10,r = 4,order_matter = TRUE,with_repetition = FALSE)
#> [1] 5040

Order does not matter with repetition

\[\frac{(n+r-1)!}{r!(n-1)!}.\]

calc_combination(n = 10,r = 4,order_matter = FALSE,with_repetition = TRUE)
#> [1] 715

Order does not matter without repetition

\[\frac{n!}{r!(n-r)!}.\]

calc_combination(n = 10,r = 4,order_matter = FALSE,with_repetition = FALSE)
#> [1] 210

calc_correlation

The goal of calc_correlation is to compute associations metrics.

Kendall

The Kendall correlation coefficient, also known as the Kendall’s Tau coefficient, measures the relationship between two ranked variables.

Maurice Kendall created it, and it is especially useful for analyzing non-linear relationships or ranked data. The coefficient is calculated by counting the number of concordant pairs (ranks in the same order) and discordant pairs (ranks in opposite order) in the data.

\[\frac{n_c-n_d}{\frac{1}{2}*n(n/1)},\] where:

  • \(n_c\) is the number of concordant observations;
  • \(n_d\) is the number of discordant observations;
  • \(n\) is the number of observations.
calc_correlation(mtcars$hp,mtcars$drat,type = "kendall")
#> [1] -0.3826269

Pearson

The Pearson correlation coefficient quantifies the linear relationship that exists between two continuous variables. It ranges from -1 to 1, indicating the association’s strength and direction.

A value of 1 indicates a perfect positive linear relationship, a value of -1 indicates a perfect negative linear relationship, and a value of 0 indicates no linear relationship.

\[\frac{\sigma_{xy}}{\sigma_x\sigma_y},\] where:

  • \(\sigma_{xy}\) is the covariance of \(x\) and \(y\);
  • \(\sigma_{x}\) is the variance of \(x\);
  • \(\sigma_{y}\) is the variance of \(y\).
calc_correlation(mtcars$hp,mtcars$drat,type = "pearson")
#> [1] -0.4487591

Spearman

The Spearman correlation coefficient assesses the strength and direction of a monotonic relationship between two variables, regardless of whether it is linear or non-linear.

It also has a value between -1 and 1, with 1 representing a perfect monotonic relationship and -1 representing a perfect inverse monotonic relationship. A value of 0 indicates that there is no monotonic relationship.

\[1- \frac{6\sum\limits_{i=1}^{n}d_i^2}{n(n^2-1)},\]

where:

  • \(d_i\) is the difference between the ranks of \(x\) and \(y\);
  • \(n\) is the number of observations.
calc_correlation(mtcars$hp,mtcars$drat,type = "spearman")
#> [1] -0.520125

calc_cv

The goal of calc_cv is to compute the coefficient of variation (CV), given by:

\[\frac{s}{\bar{x}},\] where:

  • \(s\) is the sample standard deviation;
  • \(\bar{x}\) is the sample mean.
set.seed(123);x <- rexp(n = 100)

calc_cv(x)
#> [1] 0.99

If you set the argument as_perc to TRUE, the CV will be multiplied by 100.

calc_cv(x,as_perc = TRUE)
#> [1] 99.32

calc_error

The goal of calc_error is to compute errors metrics.

Mean Absolute Error (MAE)

MAE measures the average absolute difference between the predicted and actual values:

\[\frac{\sum\limits_{i=1}^{n}|X_i-Y_i|}{n}.\]

Mean Absolute Percentage Error (MAPE)

MAPE measures the average percentage difference between the predicted and actual values relative to the actual values:

\[\frac{\sum\limits_{i=1}^{n}\left|\frac{X_i-Y_i}{X_i}\right|}{n}.\]

Mean Squared Error (MSE)

MSE measures the average of the squared differences between the predicted and actual values:

\[\frac{\sum\limits_{i=1}^{n}(X_i-Y_i)^2}{n}.\]

Root Mean Squared Error (RMSE)

RMSE is the square root of the MSE, providing the measure of average prediction error in the same units as the target variable:

\[\sqrt{\text{MSE}}.\]

Root Mean Squared Percentage Error (RMSPE)

RMSPE is the square root of the average of the squared percentage differences between the predicted and actual values relative to the actual values:

\[\sqrt{\frac{\sum\limits_{i=1}^{n}\left(\frac{X_i-Y_i}{X_i}\right)^2}{n}}.\]

calc_kurtosis

The goal of calc_kurtosis is to compute a kurtosis coefficient.

calc_kurtosis(x = x)
#> [1] -2.934065

Biased

The biased kurtosis coefficient, is given by:

\[\frac{\sum\limits_{i=1}^n(x_i - \bar{x})^4}{n*s_x^4},\]

where:

  • \(x_i\) is a numeric vector of length \(n\);
  • \(\bar{x}\) is the mean of \(x\);
  • \(s_x\) is the standard deviation of \(x\).
calc_kurtosis(x = x,type = "biased")
#> [1] 14.81846

Excess

The excess kurtosis coefficient, is given by:

\[\frac{\sum\limits_{i=1}^n(x_i - \bar{x})^4}{n*s_x^4}-3,\]

where:

  • \(x_i\) is a numeric vector of length \(n\);
  • \(\bar{x}\) is the mean of \(x\);
  • \(s_x\) is the standard deviation of \(x\).
calc_kurtosis(x = x,type = "excess")
#> [1] 11.81846

Percentile

The percentile kurtosis coefficient, is given by:

\[\frac{Q_3-Q_1}{P_{90}-P_{10}},\] where:

  • \(Q_1\) is the first quartile;
  • \(Q_3\) is the third quartile;
  • \(P_{90}\) is the 90th percentile;
  • \(P_{10}\) is the 10th percentile.
calc_kurtosis(x = x,type = "percentile")
#> [1] 0.3177264

Unbiased

The unbiased kurtosis coefficient, is given by:

\[\frac{(n+1)*n}{(n-1)*(n-2)*(n-3)}*\frac{\sum\limits_{i=1}^n(x_i - \bar{x})^4}{n*s_x^4} - 3*\frac{(n-1)^2}{(n-2)*(n-3)},\]

where:

  • \(x_i\) is a numeric vector of length \(n\);
  • \(\bar{x}\) is the mean of \(x\);
  • \(s_x\) is the standard deviation of \(x\).
calc_kurtosis(x = x,type = "unbiased")
#> [1] -2.934065

calc_mean

The goal of calc_mean is to compute the mean.

Arithmetic

Simple arithmetic mean

\[\frac{1}{n}\sum\limits_{i=1}^{n}x_i,\] where:

  • \(x_i\) is a numeric vector of length \(n\).
calc_mean(x = 1:10,type = "arithmetic")
#> [1] 5.5

Weighted arithmetic mean

\[\frac{1}{\sum\limits_{i=1}^{n}w_i}\sum\limits_{i=1}^{n}w_ix_i,\] where:

  • \(x_i\) is a numeric vector of length \(n\);
  • \(w_i\) is a numeric vector of length \(n\), with the respective weights of \(x_i\).
calc_mean(x = 1:10,type = "arithmetic",weight = 1:10)
#> [1] 7

Trimmed arithmetic mean 

calc_mean(x = 1:10,type = "arithmetic",trim = .4)
#> [1] 5.5

Geometric

\[\sqrt[n]{\prod\limits_{i=1}^{n}x_i} = \sqrt[n]{x_1\times x_2 \times...\times x_n},\]

where:

  • \(x_i\) is a numeric vector of length \(n\).
calc_mean(x = 1:10,type = "geometric")
#> [1] 4.528729

Harmonic

\[\frac{n}{\sum\limits_{i=1}^{n}\frac{1}{x_i}},\] where:

  • \(x_i\) is a numeric vector of length \(n\).
calc_mean(x = 1:10,type = "harmonic")
#> [1] 3.414172

calc_modality

The goal of calc_modality is to compute the number of modes.


calc_modality(x = c("a","a","b","b"))
#> [1] 2

calc_mode

The goal of calc_mode is to compute the mode.

set.seed(123);cat_var <- sample(letters,100,replace = TRUE)

table(cat_var)
#> cat_var
#>  a  b  c  d  e  f  g  h  i  j  k  l  m  n  o  p  q  r  s  t  u  v  w  y  z 
#>  1  2  5  2  4  3  6  4  5  4  3  3  3  6  4  3  3  3  4  3  4  8  3 10  4

We can see that the letter “y” appears the most, indicating that it is the variable’s mode.

calc_mode(cat_var)
#> [1] "y"

calc_peak_density

The goal of calc_peak_density is to compute the peak density value of a numeric value.

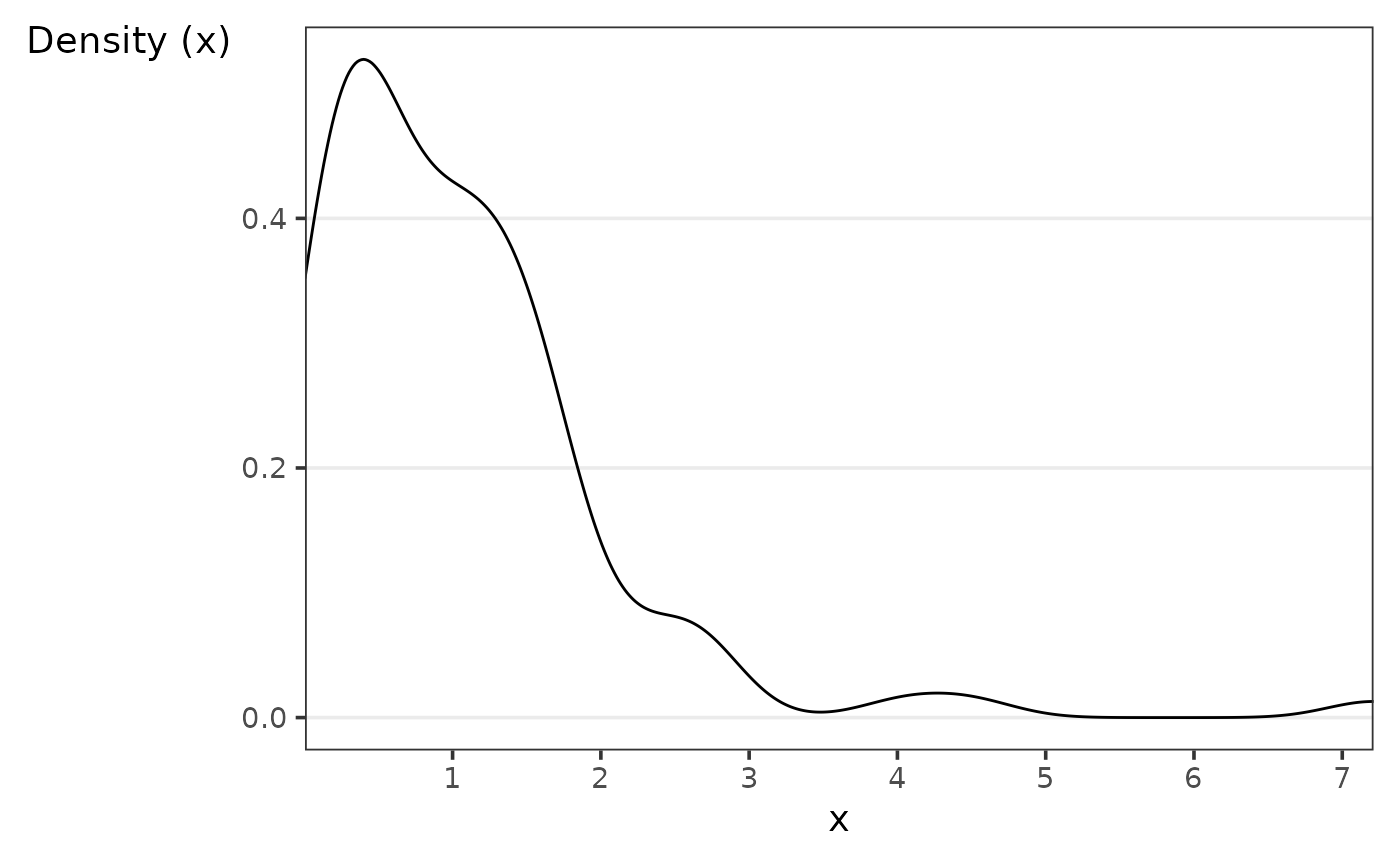
Assume we want to know what the density’s peak value is.

calc_peak_density(x)
#> [1] 0.3901813

calc_perc

The goal of calc_perc is to compute the percentage.


#without main_var
calc_perc(mtcars,grp_var = c(cyl,vs))
#> # A tibble: 5 × 4
#>     cyl    vs     n  perc
#>   <dbl> <dbl> <int> <dbl>
#> 1     8     0    14 43.8 
#> 2     4     1    10 31.2 
#> 3     6     1     4 12.5 
#> 4     6     0     3  9.38
#> 5     4     0     1  3.12

#main_var within grp_var
calc_perc(mtcars,grp_var = c(cyl,vs),main_var = vs)
#> # A tibble: 5 × 4
#> # Groups:   vs [2]
#>      vs   cyl     n  perc
#>   <dbl> <dbl> <int> <dbl>
#> 1     0     8    14 77.8 
#> 2     0     6     3 16.7 
#> 3     0     4     1  5.56
#> 4     1     4    10 71.4 
#> 5     1     6     4 28.6

#main_var not within grp_var
calc_perc(mtcars,grp_var = c(cyl),main_var = vs)
#> # A tibble: 5 × 4
#> # Groups:   vs [2]
#>      vs   cyl     n  perc
#>   <dbl> <dbl> <int> <dbl>
#> 1     0     8    14 77.8 
#> 2     0     6     3 16.7 
#> 3     0     4     1  5.56
#> 4     1     4    10 71.4 
#> 5     1     6     4 28.6

calc_skewness

The goal of calc_skewness is to compute a skewness coefficient.

calc_skewness(x = x)
#> [1] 2.74827

Where different types of coefficients are provided, they are:

Bowley

The Bowley skewness coefficient, is given by:

\[\frac{Q_3+Q_1-2Q_2}{Q_3-Q_1},\] where:

  • \(Q_1\) is the first quartile;
  • \(Q_2\) is the second quartile;
  • \(Q_3\) is the third quartile.
calc_skewness(x = x,type = "bowley")
#> [1] 0.07563213

Fisher-Pearson

The Fisher-Pearson skewness coefficient, is given by:

\[\frac{\sum_\limits{i=1}^{n}(x_i - \bar{x})^3}{n*(s_x)^3},\]

where:

  • \(\bar{x}\) is the mean of \(x\);
  • \(x_i\) is a numeric vector of length \(n\);
  • \(s_x\) is the standard deviation of \(x\).
calc_skewness(x = x,type = "fisher_pearson")
#> [1] 2.74827

Kelly

The Kelly skewness coefficient, is given by:

\[\frac{P_{90}+P_{10}-2Q_2}{P_{90}-P_{10}},\] where:

  • \(P_{90}\) is the 90th percentile;
  • \(Q_2\) is the second quartile, i.e., \(P_{50}\);
  • \(P_{10}\) is the 10th percentile;
calc_skewness(x = x,type = "kelly")
#> [1] 0.1755126

Pearson median

The Pearson median skewness coefficent, or second skewness coefficient, is given by:

\[\frac{3(\bar{x}- \tilde{x})}{s_x},\]

where:

  • \(\bar{x}\) is the mean of \(x\);
  • \(\tilde{x}\) is the median of \(x\);
  • \(s_x\) is the standard deviation of \(x\).
calc_skewness(x = x,type = "pearson_median")
#> [1] 0.5718116

Rao

The Rao skewness coefficient, is given by:

\[\frac{[n/(n-1)](\bar{x}- \tilde{x})}{\sqrt{(n-2)/n}},\]

where:

  • \(\bar{x}\) is the mean of \(x\);
  • \(\tilde{x}\) is the median of \(x\);
  • \(n\) is the length of \(x\).
calc_skewness(x = x,type = "rao")
#> [1] 0.2019945