In this post you will learn how to fraud a fraud detection.
Introduction
The Benford’s Law, also known as the first-digit law, investigates the distribution of leading digits in numerical data.
It reveals that in many naturally occurring datasets, the probability of a number having a specific first digit is not uniform; as a result, this law emphasizes the inherent characteristics and tendencies of numbers in our numerical system, revealing natural patterns.
Benford’s law equation is given by:
\[ \log_{10}\left( 1+\frac{1}{x}\right), \tag{1}\]
where \(x\) is the first digit of a number.
Let’s see how the law compares to our simulations now.
Simulated application
Exponential distribution
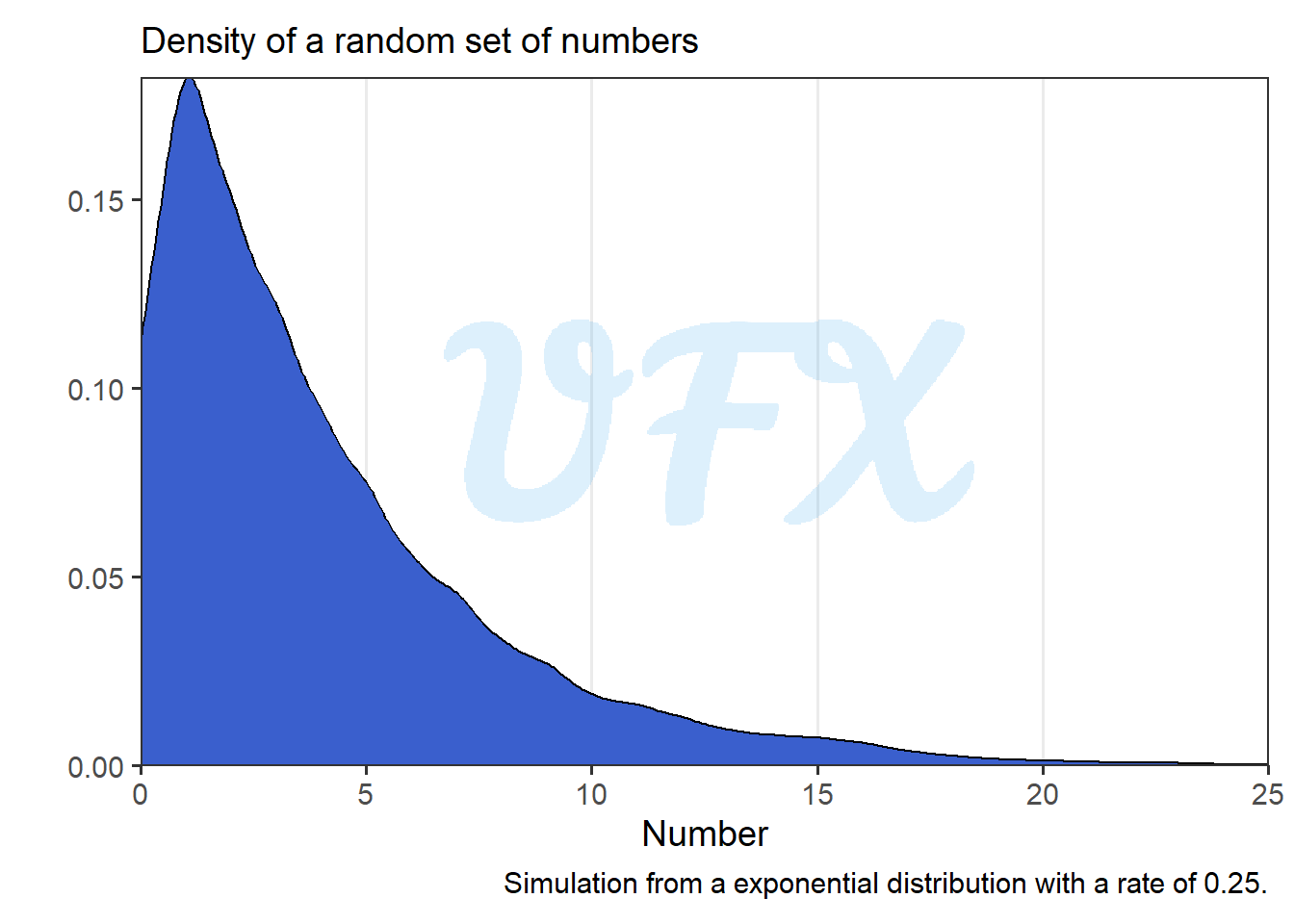
First let’s simulate a set of 10,000 random numbers from a exponential distribution with a rate of 0.25.
Next, we extract the first digit of each number and calculate the frequency of each one.
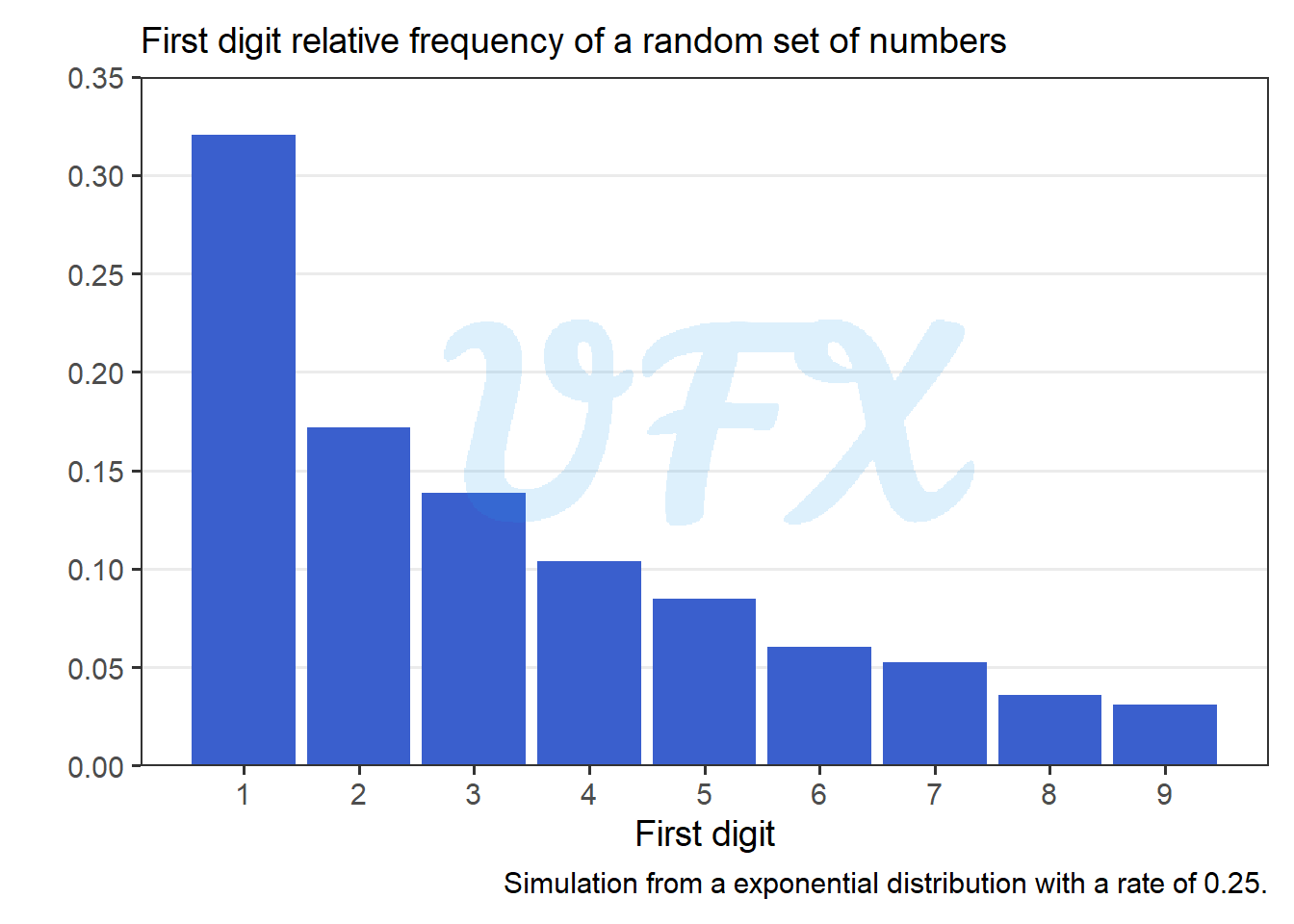
Smaller digits are more common, as shown in the graph above, and as the digit grows larger, the frequency decreases. Let us now compare the actual result to the expected result.
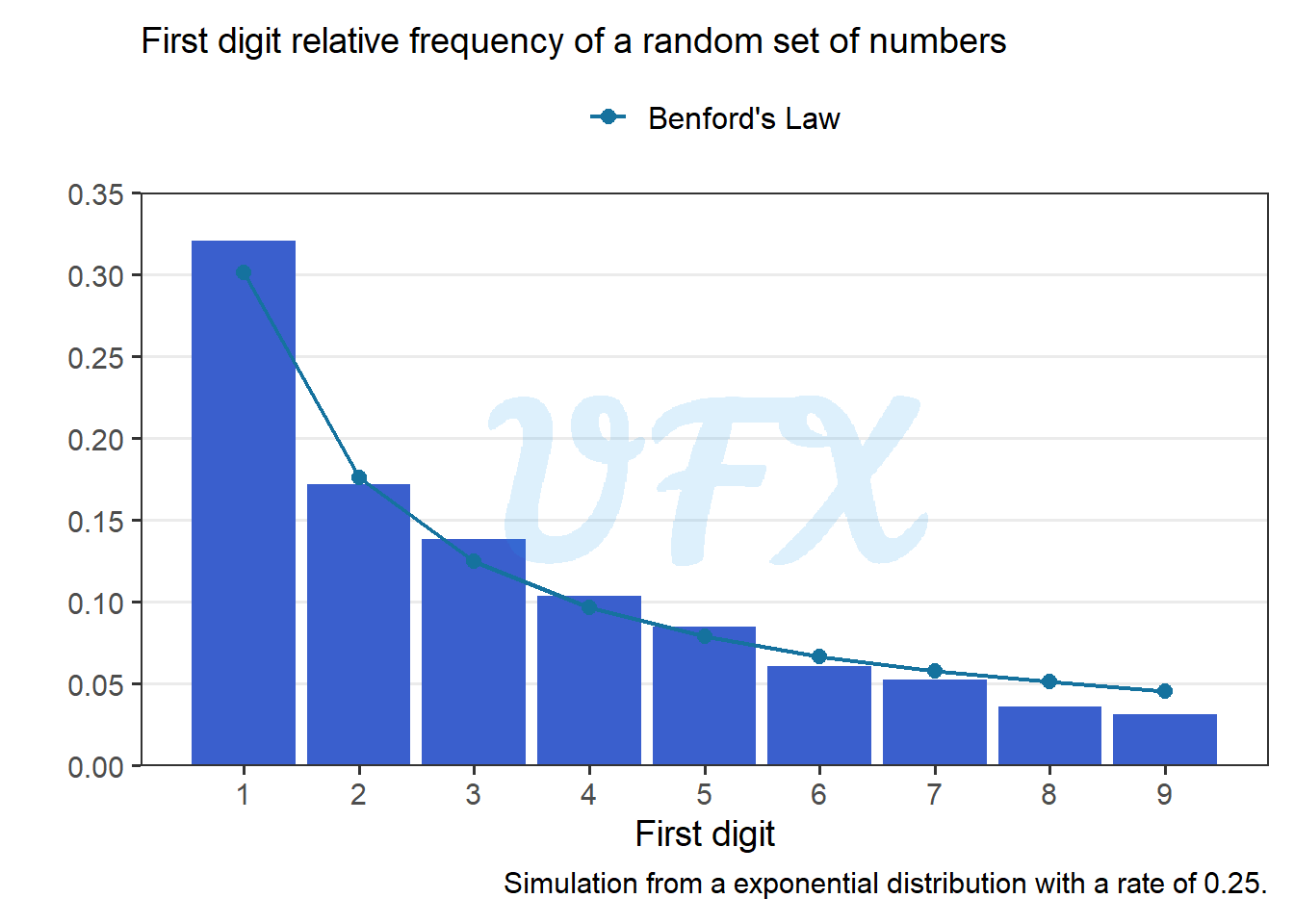
As we can see, Benford’s Law and our data are very similar, but is this always the case?
Uniform distribution
Let’s run a simulation of 10,000 random numbers drawn from a uniform distribution with a range of 1 to 100.
The simulated data is shown below:
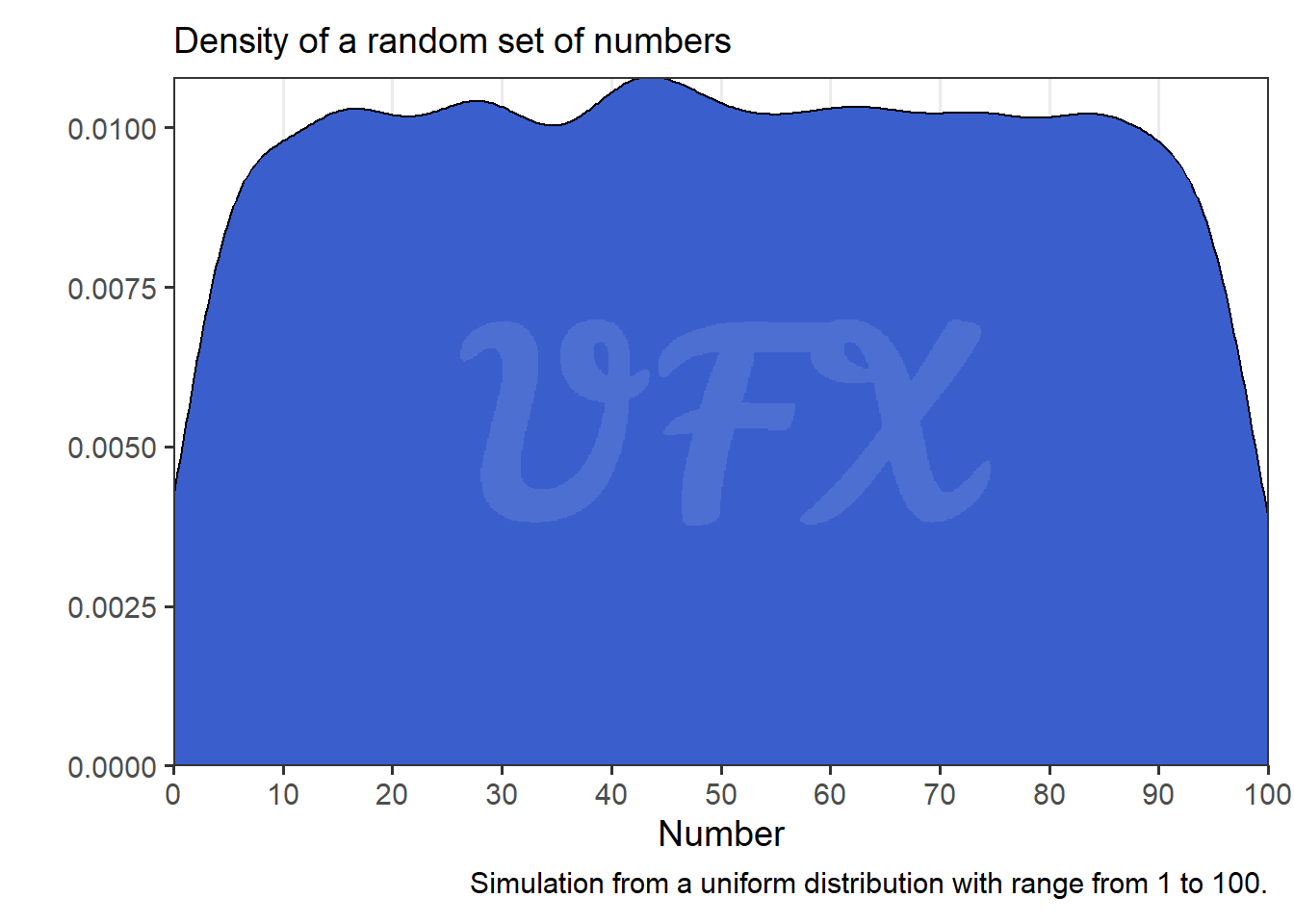
Let us now compute the frequency of the first digits.
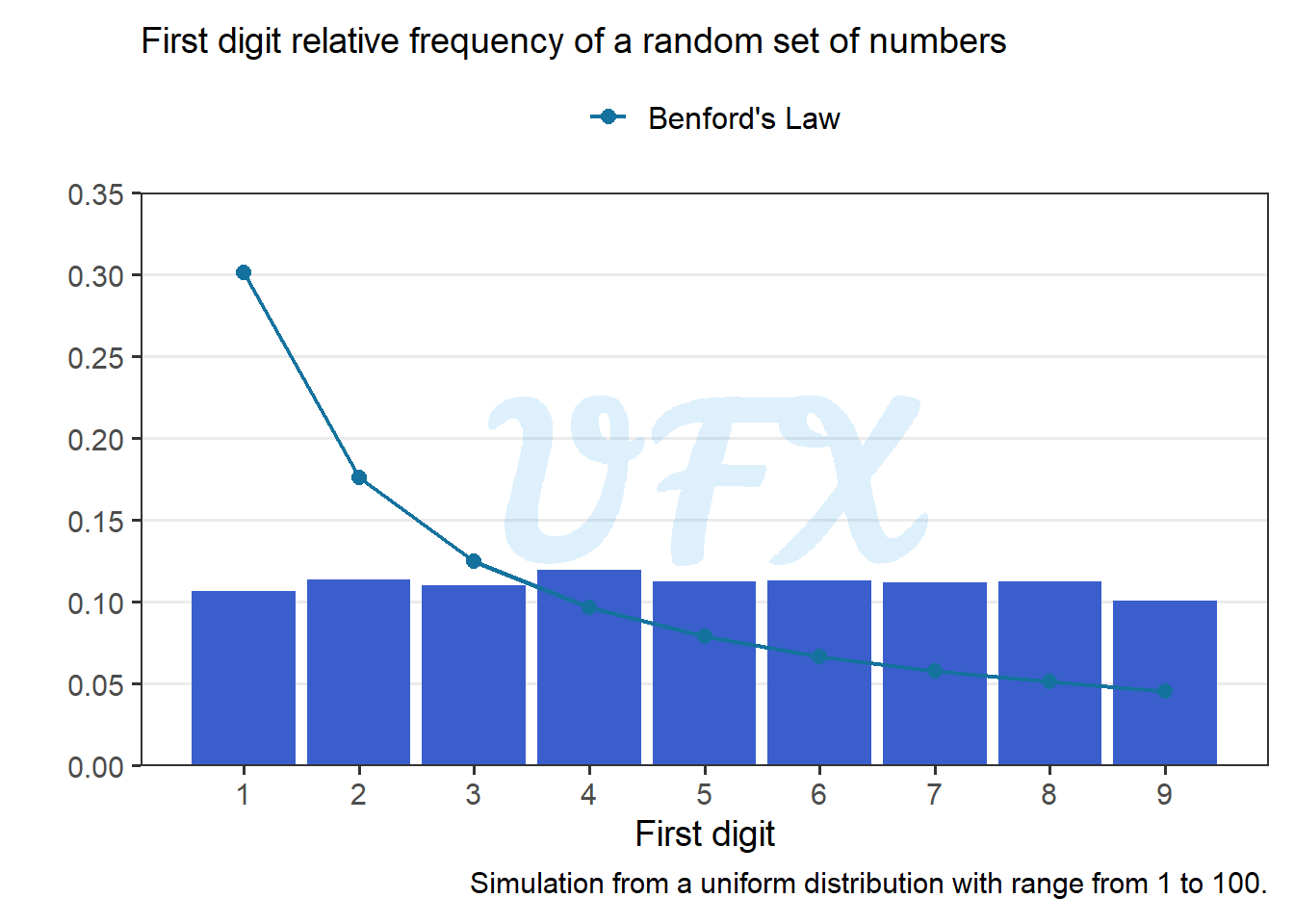
We can see now that the law differs from the simulated data, but why? Because we are sampling from a set of numbers where the first digit pool is uniform.
Considerations
Benford’s Law is applicable to datasets with broad value ranges but may not work well with datasets with narrow value ranges.
Because its distribution patterns are sensitive to data scale, it is less effective when data is not spread across multiple orders of magnitude. Intentional data manipulation can reduce the accuracy of fraud detection, necessitating the use of additional investigative techniques.
While it primarily analyzes first digits, it can also analyze second and subsequent digits, though with potentially less robust results.
Benford’s Law should be used with caution, taking into account the specific data context, because different data types exhibit different statistical patterns, and blind application may result in incorrect conclusions.